Izliekti daudzstūri. Izliekta daudzstūra definīcija. Izliekta daudzstūra diagonāli

Šie ģeometriskie skaitļi mūs apkārt ieskauj visur. Izliektie daudzstūri ir dabīgi, piemēram, bišu medus vai mākslīgie (ko rada cilvēki). Šie skaitļi tiek izmantoti dažāda veida pārklājumu ražošanai, krāsošanai, arhitektūrai, rotājumiem utt. Izliektajiem daudzstūra elementiem ir īpašība, ka visi to punkti atrodas vienā līnijas pusē, kas iziet cauri šīs ģeometriskās figūras blakus esošajām virsotnēm. Ir citas definīcijas. Izliekts ir tas daudzstūris, kas atrodas vienā pusplaknē attiecībā pret jebkuru līniju, kurā ir viena no tās malām.

Izliekti daudzstūri

Pamata ģeometrijas gaitā vienmērmēs uzskatām tikai vienkāršus daudzstūrus. Lai izprastu visas šo ģeometrisko rādītāju īpašības, ir jāsaprot to raksturs. Vispirms jāsaprot, ka jebkura līnija, kuras galus sakrīt, tiek saukta par slēgtu. Un no tā izveidotā skaitļa var būt dažādas konfigurācijas. Daudzstūris ir vienkārša slēgta daudzstūra līnija, kuras blakus esošās saites atrodas uz vienas līnijas. Tās saites un virsotnes ir attiecīgi šīs ģeometriskās figūras puses un virsotnes. Vienkāršā polilēnei nedrīkst būt pašrezerves.

Daudzstūra virsotnes sauc par blakusja tie pārstāv vienas no tās pusēm. Ģeometriskā figūra, kurai ir n-to virsotņu skaits, un līdz ar to arī n-to pušu skaits, tiek saukta par n-gonu. Šķelto līniju sauc par šīs ģeometriskās figūras robežu vai kontūru. Daudzstūra plakne vai plaknes daudzstūris saucas par ierobežotu daļu no jebkuras plaknes, kuru tā ir ierobežojusi. Šīs ģeometriskās figūras kaimiņu malas ir sadalītas līnijas segmenti, sākot no vienas virsotnes. Viņi nebūs kaimiņi, ja tie nāk no dažādām daudzstūra virsotnēm.

Citas izliekta daudzstūra definīcijas

Elementārajā ģeometrijā ir vēl vairākkas ir līdzvērtīgs definīciju nozīmē, norādot, kurš daudzstūris saucas izliekts. Un visi šie formulējumi ir vienādi patiesi. Iecēlīgs daudzstūris tiek uzskatīts par:

• katrā segmentā, kas savieno visus divus punktus tajā, tas ir pilnībā;

• tajā atrodas visas tās diagonāles;

• jebkurš iekšējais leņķis nepārsniedz 180 °.

Daudzstūra vienmēr dala plakni ar 2daļas. Viens no tiem ir ierobežots (tas var būt aplis), un otrs ir neierobežots. Pirmais tiek saukts par iekšējo reģionu, otro sauc par šī ģeometriskā figūra ārējo reģionu. Šis daudzstūris ir vairāku puslīniju krustpunkts (citiem vārdiem - kopējā sastāvdaļa). Šajā gadījumā tas pilnībā pieder pie katra segmenta, kas beidzas ar punktiem, kas pieder poligonam.

Izliektā daudzstūra šķirnes

Izliektā daudzstūra definīcija nenorādauz to, ka ir daudz veidu. Un katram no tiem ir noteikti kritēriji. Tādējādi izliektie daudzstūri, kuru iekšējais leņķis ir vienāds ar 180 °, sauc vāji izliekti. Izliekta ģeometrisko skaitlis, kas ir trīs virsotnes, sauc par trīsstūri, četri - četrstūris, pieci - piecstūri, uc Katrs no izliekta n-gons atbilst šādām svarīgas prasības: .. N ir vienāds vai lielāks par 3. Katrs no trijstūriem ir izliekta. Šī veida ģeometriskā figūra, kurā visas virsotnes atrodas vienā lokā, tiek saukts par apzīmējumu. Apzīmē izliektu daudzstūri, ja visas tā malas pie apļa pieskaras tai. Divus daudzstūrisus sauc par vienādiem tikai tad, ja tos var apvienot ar pārklājuma palīdzību. Daudzstūra plakni sauc par plaknes daudzstūri (plaknes daļa), ko ierobežo šis ģeometriskais skaitlis.

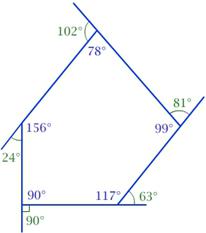
Regulāri izliekti daudzstūri

Tiek saukti pareizi daudzstūriģeometriski skaitļi ar vienādiem leņķiem un malām. To iekšpusē ir punkts 0, kas atrodas tajā pašā attālumā no katras tā virsotnes. To sauc par šī ģeometriskā skaitļa centru. Segmentus, kas savieno centru ar šīs ģeometriskās figūras virsotnēm, sauc par apophemām, un tie, kas savieno punktu 0 ar sāniem, ir rādiusi.

Labais četrstūris ir kvadrāts. Labais trīsstūris saucas par vienādmalu. Šādām figūrām ir šāds noteikums: katru izliektā daudzstūra leņķi ir 180 ° * (n-2) / n,

kur n ir šī izliektā ģeometriskā skaitļa virsotņu skaits.

Jebkura regulārā daudzstūra platība ir noteikta pēc formulas:

S = p * h,

kur p ir vienāds ar pusi no dotā daudzstūra daudzuma, un h ir vienāds ar apophema garumu.

Izliekto daudzstūru īpašības

Izliektajām daudzstūmēm ir noteiktas īpašības. Tātad segmentā, kas savieno jebkurus divus punktus ar šādu ģeometrisko skaitli, noteikti atrodas tajā. Pierādījums:

Pieņemsim, ka P ir dots izliektsdaudzstūris Paņem divus patvaļīgus punktus, piemēram, A un B, kas pieder P. Ar pašreizējo definīciju izliekta daudzstūra, šie punkti atrodas vienā pusē no taisnas līnijas, kas satur jebkuru virzienu R. Tātad AB ir arī šo īpašumu, un ir ietverta R. izliekts daudzstūris vienmēr Absolūti visas diagonāles, kas ir izvilktas no vienas no tās virsotnēm, ir iespējams sadalīt vairākos trīsstūros.

Izliekto ģeometrisko figūru leņķi

Izliekta daudzstūra leņķi ir leņķi, kaveido tās puses. Iekšējie stūri atrodas šīs ģeometriskās figūras iekšējā daļā. Leņķis, ko veido tā sāni, kas saplūst vienā virsotnē, sauc par izliektā daudzstūra leņķi. Leņķi, kas atrodas blakus konkrētā ģeometriskā skaitļa iekšējiem stūriem, sauc par ārējiem. Katrs tajā izliektā daudzstūra leņķis ir vienāds ar:

180 ° - x,

kur x ir ārējā leņķa vērtība. Šī vienkāršā formula attiecas uz visiem šāda veida ģeometriskiem skaitļiem.

Vispārīgā gadījumā pastāv ārējie leņķišāds noteikums: katrs izliekta daudzstūra leņķis ir vienāds ar starpību starp 180 ° un iekšējā leņķa vērtību. Tam var būt vērtības diapazonā no -180 ° līdz 180 °. Tāpēc, ja iekšējais leņķis ir 120 °, ārējais leņķis ir 60 °.

Izliekto daudzstūru leņķu summa

Izliektā daudzstūra interjera leņķu summa tiek noteikta pēc formulas:

180 ° * (n-2),

kur n ir n-gona virsotņu skaits.

Tiek aprēķināta izliektā daudzstūra leņķu summagluži vienkārši. Apsveriet šādu ģeometrisko figūru. Lai noteiktu izliektā daudzstūra iekšējo leņķu summu, vienai no tās virsotnēm jābūt savienotām ar citām virsotnēm. Šīs darbības rezultātā iegūstam (n-2) trijstūri. Ir zināms, ka jebkuras trīsstūra leņķu summa vienmēr ir 180 °. Tā kā to skaits katrā poligonā ir vienāds ar (n-2), šādas skaitļa iekšējo leņķu summa ir 180 ° x (n-2).

Izliektā daudzstūra leņķu summa, viz.visi divi iekšējie un blakus esošie ārējie leņķi, šis izliekts ģeometriskais rādītājs vienmēr būs 180 °. Pamatojoties uz to, ir iespējams noteikt visu tā leņķu summu:

180 x n

Iekšējo leņķu summa ir 180 ° * (n-2). Pamatojoties uz to, dotā skaitļa visu ārējo leņķu summa tiek noteikta pēc formulas:

180 ° * n-180 ° - (n-2) = 360 °.

Jebkuras izliekta daudzstūra ārējo leņķu summa vienmēr ir 360 ° (neatkarīgi no tā malu skaita).

Izliektā daudzstūra ārējais leņķis parasti ir starpība starp 180 ° un iekšējā leņķa vērtību.

Citas izliekta daudzstūra īpašības

Papildus šo ģeometrisko pamatīpašībāmcipari, viņiem ir citi, kas rodas manipulējot ar viņiem. Tādējādi jebkuru poligonu var sadalīt vairākās izliektajās n-gonās. Šim nolūkam ir nepieciešams turpināt katru no savām malām un samazināt šo ģeometrisko skaitli gar šīm taisnām līnijām. Sadalīt jebkuru poligonu vairākās izliektām daļām ir iespējams, un, lai top par katru no gabaliem sakrīt ar visiem tās virsotnes. No šī ģeometriskā skaitļa ir ļoti vienkārši izveidot trijstūri, turot visas diagonāles no vienas virsotnes. Tādējādi, jebkurš daudzstūris, galu galā, var iedalīt noteiktam skaitam trijstūriem, kas ir ļoti noderīga, risinot dažādus uzdevumus, kas saistīti ar šādiem ģeometriskās formas.

Izliekta daudzstūra perimetrs

Polilīna gabali, ko sauc par sāniemdaudzstūris, ko visbiežāk apzīmē ar šādiem burtiem: ab, bc, cd, de, ea. Tie ir ģeometriskās figūras puses ar virsotnēm a, b, c, d, e. Visa šī izliektā daudzstūra daudzuma garuma summa tiek saukta par tās perimetru.

Daudzstūra aplis

Izliekti daudzstūri var būt uzrakstīti unaprakstīts. Tajā tiek saukts aplis, kas pieskaras visām ģeometriskās figūras malām. Šādu daudzstūri sauc aprakstīts. Apļa, kas ir ierakstīts poligonā, centrs ir visu leņķu bisektoru krustošanās punkts noteiktā ģeometriskā skaitlī. Šāda daudzstūra platība ir vienāda ar:

S = p * r,

kur r ir ierakstītā apļa rādiuss, un p ir dotā daudzstūra puspereimeters.

Aplis, kurā ir daudzstūra virsotnes,kas aprakstīts tuvumā. Šajā gadījumā šo izliektā ģeometriskā figūra tiek saukta par uzrakstītu. Apļa centrs, kas aprakstīts pie šāda daudzstūra, apzīmē punktu, kurā krustojas tā sauktie vidējie perpendikulāri no visām pusēm.

Izliekto ģeometrisko figūru diagonāli

Izliekta daudzstūra diagonāli ir segmenti,kas savieno ne blakus esošās virsotnes. Katrs no tiem atrodas šajā ģeometriskā skaitā. Šāda n-gona diagonāļu skaits tiek noteikts pēc formulas:

N = n (n-3) / 2.

Izgulstas daudzstūra diagonāļu skaits spēlēsvarīga loma elementārajā ģeometrijā. Trijstūra (K) skaits, kurā var izdalīt katru izliektā daudzstūri, aprēķina pēc šādas formulas:

K = n - 2.

Izliektā daudzstūra diagonāļu skaits vienmēr ir atkarīgs no tā virsotņu skaita.

Izliekta daudzstūra sadalīšana

Dažos gadījumos, lai atrisinātu ģeometriskoizliekta daudzstūris ir jāšķiro vairākos trijstūros ar nesaistītām diagonālēm. Šo problēmu var atrisināt, iegūstot noteiktu formulu.

Problēmas definīcija: mēs saucam par noteiktu izliektā n-gona sadalījumu vairākos trīsstūros pa diagonāles, kas šķērso tikai šī ģeometriskā skaitļa virsotnēs.

Risinājums: Pieņemsim, ka P1, P2, P3, ..., Pn - augšdaļa n-gon. Numurs Xn ir tā nodalījumu skaits. Mēs rūpīgi apsveram iegūto ģeometriskā skaitļa Pi Pn diagonāli. Jebkurā no regulārajiem starpsienām P1 Pn pieder konkrētai trīsstūra P1 Pi PN, kurā 1 <i <n. Pamatojoties uz šo un pieņemot, ka i = 2,3,4, ..., n-1, kas iegūts, (n-2) no šīm starpsienām, kas iekļautas visos iespējamos īpašos gadījumos.

Ļaujiet i = 2 būt par vienu regulāru grupukas vienmēr satur diagonāli P2 Pn. Starp tajā ietilpstošo starpsienu skaits sakrīt ar (n-1) -gon P2 P3 P4 ... Pn starpsienu skaitu. Citiem vārdiem sakot, tas ir vienāds ar Xn-1.

Ja i = 3, tad šī cita starpsienu grupa būsvienmēr ir diagonāles P3 P1 un P3 Pn. Turklāt šajā grupā ietilpstošo regulāro starpsienu skaits sakrīt ar starpsienu skaitu (n-2) -gon P3 P4 ... Pn. Citiem vārdiem sakot, tas būs vienāds ar Xn-2.

Ļaujiet i = 4, tad starp trijstūriem regulārisadalīšanās noteikti saturēs trijstūri P1 P4 Pn, pie kura atrodas četrstūris P1 P2 P3 P4, (n-3) -gon P4 P5 ... Pn. Šādu četrstūristisko regulāro starpsienu skaits ir vienāds ar X4 un starpsienu skaits (n-3) -gon ir vienāds ar Xn-3. Pamatojoties uz visu iepriekš minēto, varam teikt, ka šajā grupā ietilpstošo regulāro starpsienu kopējais skaits ir Xn-3 X4. Citas grupas, kurām i = 4, 5, 6, 7 ... satur regulārus starpsienas Xn-4 X5, Xn-5 X6, Xn-6 X7 ....

Pieņemsim, ka i = n-2, tad noteiktā grupā esošo regulāro starpsienu skaits sakrīt ar partiju skaitu grupā, kurai i = 2 (citiem vārdiem sakot, tas ir vienāds ar Xn-1).

Tā kā X1 = X2 = 0, X3 = 1 un X4 = 2, ..., skaits starpsienām izliekts daudzstūris ir:

Xn = Xn-1 + Xn-2 + Xn-3 X4 + Xn-4 X5 + ... + X 5 Xn-4 + X4 Xn-3 + Xn-2 + Xn-1.

Piemērs:

X5 = X4 + X3 + X4 = 5

X6 = X5 + X4 + X4 + X5 = 14

X7 = X6 + X5 + X4 * X4 + X5 + X6 = 42

X8 = X7 + X6 + X5 * X4 + X4 * X5 + X6 + X7 = 132

Regulāro starpsienu skaits, kas šķērso vienu diagonāli

Konkrētu gadījumu pārbaudē var secināt, ka izliekto n-gonu diagonāļu skaits ir vienāds ar visu šī skaitļa starpsienu rezultātu ar (n-3).

Pierādījums šim pieņēmumam: iedomāties ka P1n = Xn * (n-3), tā kā jebkurš n-gon var sadalīt (n-2) ir trīsstūra. Šajā gadījumā viens no tiem var sakraut (n-3) -chetyrehugolnik. Tajā pašā laikā, katrs kvadrāts ir pa diagonāli. Tā kā šī izliektu ģeometrisko skaitlis divas diagonāles var tikt veikta, kas nozīmē, ka jebkurš (n-3) -chetyrehugolnikah var veikt papildu diagonāle (n-3). Pamatojoties uz to, mēs varam secināt, ka jebkurā pareizu nodalījumā ir iespēju (n-3) -diagonali atbilst šī uzdevuma prasībām.

Izliekto daudzstūru telpa

Bieži vien, risinot dažādas problēmas, elementārāģeometrija kļūst nepieciešams, lai noteiktu zonu izliekts daudzstūris. Pieņemt, ka (XI Yi.), I = 1,2,3 ... n apzīmē secību koordinātas visu kaimiņu apgabala virsotnes, kam nav self-krustojumu. Šajā gadījumā, tā laukumu aprēķina, izmantojot šādu formulu:

S = 1 (Σ (X_i + X_{i + 1}) (Y_i + Y_{i + 1}))

kur (X₁, Y.₁) = (X_{n +1}, Y._{n + 1})

</ p>