Periodiska funkcija: vispārīgie jēdzieni

Bieži vien, pētot dabas parādības, ķīmiskās undažādu vielu fizikālās īpašības, kā arī risinot sarežģītas tehniskas problēmas, ir jārisina procesi, kuru raksturīgā iezīme ir periodiskums, proti, tendence atkārtot pēc noteiktā laika posma. Šādas ciklikitātes aprakstam un grafiskajam attēlojumam zinātnē pastāv īpaša veida funkcija - periodiska funkcija.

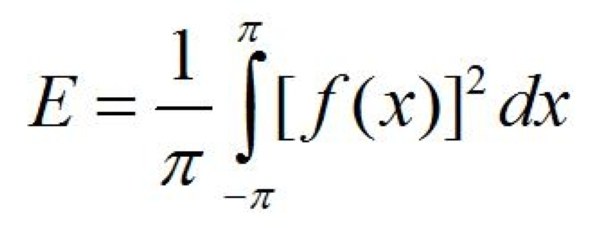
Vienkāršākais un saprotamākais piemērs ir ārstēšanano mūsu planētas ap Sauli, kur attālums starp tiem pastāvīgi seko ikgadējiem cikli. Tādā pašā veidā turbīnas asmeni atgriežas savā vietā, veicot pilnīgu apgriezienu. Visus šādus procesus var raksturot ar šādu matemātisko vērtību kā periodisku funkciju. Kopumā mūsu visa pasaule ir cikliska. Tas nozīmē, ka periodiskā funkcija arī ieņem nozīmīgu vietu cilvēka koordinātu sistēmā.

Matemātikas zinātnes nepieciešamība skaitļu teorijātopoloģija, diferenciālvienādojumi un precīzi ģeometriski aprēķini parādīja, ka XIX gadsimtā parādījās jauna funkciju kategorija ar neparastām īpašībām. Tās ir periodiskas funkcijas, kuras noteiktos punktos iegūst identiskas vērtības sarežģītu pārveidojumu rezultātā. Tagad tos izmanto daudzās matemātikas un citu zinātņu nozarēs. Piemēram, pētot dažādus vibrācijas efektus viļņu fizikā.

Tiek piedāvātas dažādas matemātiskās mācību grāmatasatšķirīga definīcija periodisku funkciju. Tomēr, neatkarīgi no šīm atšķirībām redakcijā, tie ir līdzvērtīgi, jo tie apraksta pašas īpašības funkciju. Vienkāršākais un pamanāmākā var būt šādu definīciju. Funkcija, tad summas, kas neattiecas mainīties, ja mēs pievienot savu argumentu skaits, kas nav nulle, tā saukto periods funkciju apzīmē ar burtu T sauc periodiski. Ko tas viss nozīmē praktiski?

Piemēram, vienkārša formas funkcija: y = f (x) kļūst periodiski, ja X ir noteikta perioda vērtība (T). No šīs definīcijas izriet, ka, ja fiktīvā skaitļa vērtība ar periodu (T) ir definēta vienā no punktiem (x), tā vērtība arī kļūst zināma punktos x + T, x = T. Svarīgs punkts šeit ir tas, ka tad, kad T vienība ar nulli kļūst par identitāti. Periodiskajai funkcijai var būt bezgalīgs skaits dažādu periodu. Lielākajā daļā gadījumu starp pozitīvām T vērtībām ir periods ar mazāko skaitlisko indeksu. To sauc par galveno periodu. Un visas pārējās T vērtības vienmēr ir daudzkārtīgas. Tas ir vēl viens interesants un ļoti svarīgs īpašums dažādām zinātnes jomām.

Periodiskās funkcijas grafikā ir arīvairākas pazīmes. Piemēram, ja T ir pamata periods izteiksmi: y = f (x), tad, atliekot šo funkciju, vienkārši pietiekami, lai izveidotu filiāli vienā no periodiem perioda garumu, un tad pārvietot to pa x asi par šādām vērtībām: ± T, ± 2T , ± 3T un tā tālāk. Noslēgumā jāatzīmē, ka ne visi no periodiskās funkcija ir galvenais posms. Klasisks piemērs tam ir vācu matemātiķis Dirichlet funkcija no šādā formā: y = d (x).